GetFEMによる丸棒のねじり解析

GetFEMによる丸棒のねじり解析#

本記事は Salome-Meca2019による丸棒のねじり解析をGetFEMで再現したものです．

モデルのパラメータ#

ここで，問題のさまざまな物理パラメータおよび数値パラメータを定義しましょう．

elements_degree = 1  # 次数
E = 200.0e03  # ヤング率(N/mm^2)
nu = 0.3  # ポアソン比
d = 100.0  # 直径(mm)
L = 500.0  # 高さ(mm)
T = 1.0e06  # トルク(N mm)

初期化#

Python の場合，これは簡単です． GetFEM をグローバルにインポートするだけです (NumPy と PyVista もインポートする必要があります)．

import getfem as gf
import numpy as np
import pyvista as pv

from bokeh.plotting import figure, show
from bokeh.models import ColumnDataSource, Label
from bokeh.layouts import column

pv.start_xvfb()
pv.set_jupyter_backend("panel")

メッシュ生成#

GetFEMには円筒形のメッシュを作成する機能はありません．その代わり立方体の規則的なメッシュを素早く作成する機能があるためそれを利用します． NumPyの配列からX方向長さが円筒形の半径 \(r\) ，Y方向長さが \(2\pi\) のメッシュを作成します．しかしながら，この方法ではポイントのマージがうまくいかず，断念せざるを得ませんでした．

# rhos = np.linspace(0.0001, d / 2, 8 + 1)
# phis = np.linspace(0.0, 2.0 * np.pi, 16 + 1)
# zs = np.linspace(L, 0.0, 25 + 1)
# mesh = gf.Mesh("cartesian Q1", rhos, phis, zs)
# pts = mesh.pts()
# r = pts[0]
# t = pts[1]
# z = pts[2]
# mesh.set_pts(np.array([r * np.cos(t), r * np.sin(t), z]))

そのため，メッシュをフルスクラッチで作成をしました．

rhos = np.linspace(0.0001, d / 2, 8 + 1)
phis = np.linspace(0.0, 2.0 * np.pi, 16 + 1)
zs = np.linspace(L, 0.0, 25 + 1)
mesh = gf.Mesh("empty", 3)

rho_as = rhos[:-1]
rho_bs = rhos[1:]
phi_as = phis[:-1]
phi_bs = phis[1:]
z_as = zs[:-1]
z_bs = zs[1:]

for z_a, z_b in zip(z_as, z_bs):
    for phi_a, phi_b in zip(phi_as, phi_bs):
        for rho_a, rho_b in zip(rho_as, rho_bs):
            mesh.add_convex(
                gf.GeoTrans("GT_QK(3,1)"),
                [
                    [
                        rho_a * np.cos(phi_a),
                        rho_a * np.cos(phi_b),
                        rho_b * np.cos(phi_a),
                        rho_b * np.cos(phi_b),
                        rho_a * np.cos(phi_a),
                        rho_a * np.cos(phi_b),
                        rho_b * np.cos(phi_a),
                        rho_b * np.cos(phi_b),
                    ],
                    [
                        rho_a * np.sin(phi_a),
                        rho_a * np.sin(phi_b),
                        rho_b * np.sin(phi_a),
                        rho_b * np.sin(phi_b),
                        rho_a * np.sin(phi_a),
                        rho_a * np.sin(phi_b),
                        rho_b * np.sin(phi_a),
                        rho_b * np.sin(phi_b),
                    ],
                    [z_a, z_a, z_a, z_a, z_b, z_b, z_b, z_b],
                ],
            )

ちなみに

節点数と要素数を確認すること．

メッシュの描画#

メッシュをプレビューし，その妥当性を制御するために，次の手順を使用します．外部グラフィカルポストプロセッサPyVistaを使用する必要があります．

mesh.export_to_vtk("mesh.vtk", "ascii")

a = [d / 2.0, 0.0, 0.0]
b = [d / 2.0, 0.0, L]
line = pv.Line(a, b)

m = pv.read("mesh.vtk")
plotter = pv.Plotter()
plotter.add_mesh(m, show_edges=True)
plotter.add_mesh(line, color="white", line_width=10)
plotter.add_point_labels(
    [a, b], ["A", "B"], font_size=48, point_color="red", text_color="red"
)
plotter.enable_parallel_projection()
plotter.show(cpos="yz")

ちなみに

上に示したジオメトリはインタラクティブです．また、平行投影を有効にします．ドキュメントでは，平行投影は有効ではありません． A-Bは結果のデータ抽出に使用する線です．

境界の選択#

境界のそれぞれの部分には異なる境界条件を設定するため，境界のさまざまな部分には番号を付けます．したがって，メッシュ上の要素面を選択し，メッシュ領域を定義する必要があります． 1, 2はそれぞれ上境界，下境界です．これらの境界番号は，モデルのブリックで使用されます．

fb1 = mesh.outer_faces_with_direction([0.0, 0.0, 1.0], 0.01)
fb2 = mesh.outer_faces_with_direction([0.0, 0.0, -1.0], 0.01)

TOP_BOUND = 1
BOTTOM_BOUND = 2

mesh.set_region(TOP_BOUND, fb1)
mesh.set_region(BOTTOM_BOUND, fb2)

有限要素法と積分法の定義#

メッシュをプレビューし，その妥当性を制御するために，次の手順を使用します．有限要素法を定義します．変位フィールドを近似する最初の1つは，変位フィールドを近似する mfu です．これはベクトルフィールドでPythonでは次のように定義されます．

mfu = gf.MeshFem(mesh, 3)
mfu.set_classical_fem(elements_degree)

ここで， 3 はベクトル場の次元を表します．2行目は，使用する有限要素を設定します． classical_finite_element は，連続したLagrange要素を意味し， elements_degree は 2 に設定されています．これは2次の (アイソパラメトリック) 要素を使用することを意味します． GetFEM では，既存の有限要素法を幅広く選択肢できます．付録A.有限要素法リストを参照してください．しかし，実際には Lagrange 有限要素法が最も使用されています．

次に定義するのは，積分法 mim です． GetFEM にデフォルトの積分法はありません．したがって，これは積分法を定義するためには必須です．もちろん，積分法の次数は，選択された有限要素法に好都合な積分を行うため，十分に選定しなければなりません．ここでは，完全積分を選択します。

mim = gf.MeshIm(
    mesh,
    gf.Integ(
        "IM_PRODUCT(IM_PRODUCT(IM_GAUSS1D("
        + str(elements_degree + 2)
        + "), IM_GAUSS1D("
        + str(elements_degree + 2)
        + ")), IM_GAUSS1D("
        + str(elements_degree + 2)
        + "))"
    ),
)

モデルの定義#

GetFEM のモデルオブジェクトは(未知)変数，データ，およびモデルブリックと呼ばれるものの集まりです．モデルブリックは，単一の変数か，複数の変数をリンクしているモデルの一部 (線形または非線形項) です．これらは，(接線) 線形システムの構築のために使用されます (詳細については modelオブジェクトを参照してください)．

計算される1つのフィールドに対応する1つの変数を持つ実際のモデルを宣言してみましょう．

md = gf.Model("real")
md.add_fem_variable("u", mfu)
md.add_initialized_data("data_E", E)
md.add_initialized_data("data_nu", nu)

弾性変形問題#

ここでは，弾性変形問題から始めましょう．以下の add_isotropic_linearized_elasticity_brick によって追加されている定義済みのブリックを使用します．この追加を接線線形システムに対して行います．このモデルブリックを使用するために， Lamé 係数に対応するデータは，最初にモデルに追加する必要があります．ここでは， Lamé 係数は，領域に対して一定です．以下のプログラムは，全体の弾性変形方程式を考慮に入れることができます．

md.add_isotropic_linearized_elasticity_pstress_brick(mim, "u", "data_E", "data_nu")

下側の境界に Dirichlet 条件を規定するために，既定のブリックを使用します． Dirichlet条件を定義するいくつかのオプションがあります( Dirichlet条件ブリック要素を参照)．

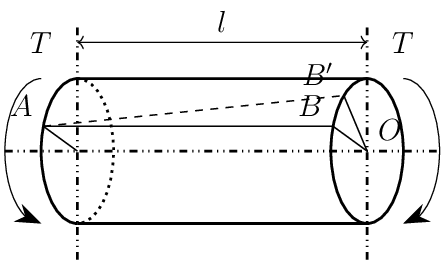
半径方向の単位ベクトル \(P\) は以下の式であらわされます．

\[ P＝\begin{pmatrix}\cos \theta &\sin \theta \end{pmatrix} \]

ベクトル \(P\) を角度 \(\theta\) で微分すると接線方向の単位ベクトルを得ることができます．

\[ \frac{dP}{d\theta }=\begin{pmatrix}-\sin \theta &\cos \theta \end{pmatrix} \]

Figure made with TikZ

md.add_initialized_data("r2", [0.0, 0.0, 0.0])
md.add_initialized_data("H2", [[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0]])
md.add_generalized_Dirichlet_condition_with_multipliers(
    mim, "u", mfu, BOTTOM_BOUND, "r2", "H2"
)

tau = 16.0 * T / np.pi / d**3
radius = d / 2.0

md.add_linear_term(
    mim, str(tau / radius) + "*" + "[-X(2), X(1), 0.0].Test_u", TOP_BOUND
)

Trace 2 in getfem_models.cc, line 4401: Mass term assembly for Dirichlet condition
Trace 2 in getfem_models.cc, line 4438: Source term assembly for Dirichlet condition

-1

モデルの求解#

モデルを正しく定義したら，次のようにして簡単に解くことができます．

md.solve()

Trace 2 in getfem_models.cc, line 3478: Linearized isotropic elasticity: generic matrix assembly
Trace 2 in getfem_models.cc, line 4401: Mass term assembly for Dirichlet condition
Trace 2 in getfem_models.cc, line 4438: Source term assembly for Dirichlet condition
Trace 2 in getfem_models.cc, line 3310: Generic source term assembly
Trace 2 in getfem_models.cc, line 3321:  (source term): generic source term assembly

(0, 1)

解のエクスポート/可視化#

以上で有限要素問題が解けました．図のように解をプロットすることができます．

U = md.variable("u")
mfu.export_to_vtk("displacement.vtk", "ascii", mfu, U, "u")

displacement = pv.read("displacement.vtk")
plotter = pv.Plotter()
plotter.add_mesh(displacement.warp_by_vector("u", factor=1000.0), show_edges=True)
plotter.enable_parallel_projection()
plotter.show(cpos="yz")

ちなみに

上に示したジオメトリはインタラクティブです．また、平行投影を有効にします．ドキュメントでは，平行投影は有効ではありません．

G = E / (2.0 * (1.0 + nu))
Ip = np.pi * d**4 / 32.0
phi = T * L / (G * Ip)
theory = (d / 2) * phi

line = displacement.sample_over_line(a, b)
distance = line["Distance"]
u = line["u"]

# create a figure
p = figure(
    title="Displacement vs Axial distance",
    x_axis_label="Axial distance (mm)",
    y_axis_label="Displacement (mm)",
)

# create ColumnDataSource
source = ColumnDataSource(
    dict(
        distance=distance, x_direction=u[:, 0], y_direction=u[:, 1], z_direction=u[:, 2]
    )
)

# plot the lines
p.line(
    x="distance",
    y="x_direction",
    source=source,
    legend_label="x direction",
    line_color="blue",
    line_width=3,
)
p.line(
    x="distance",
    y="y_direction",
    source=source,
    legend_label="y direction",
    line_color="green",
    line_width=3,
)
p.line(
    x="distance",
    y="z_direction",
    source=source,
    legend_label="z direction",
    line_color="red",
    line_width=3,
)

# add marker for theory
p.circle(x=[L], y=[-theory], size=10, color="black", legend_label="theory")

# add labels for marker
theory_label = Label(
    x=L, y=-theory, text="theory", text_color="black", x_offset=5, y_offset=-10
)
p.add_layout(theory_label)

# display legend
p.legend.location = "top_left"

# show the plot
show(column(p))

GetFEMによる丸棒のねじり解析

目次

GetFEMによる丸棒のねじり解析#

モデルのパラメータ#

初期化#

メッシュ生成#

メッシュの描画#

境界の選択#

有限要素法と積分法の定義#

モデルの定義#

弾性変形問題#

モデルの求解#

解のエクスポート/可視化#